A pesar de vivir actualmente en el momento más tecnológico de la historia, todos los años los docentes en matemáticas nos enfrentamos a esta (eterna) pregunta: ¿para qué sirven las mátemáticas? Lamentablemente, se ha llegado incluso a cuestionar la importancia de las matemáticas en la educación básica, como por ejemplo con el siguiente tweet que se hizo viral.
Otro día más sin utilizar el mínimo común múltiplo ni el máximo común divisor.
— the van (@davidmartinyo) August 29, 2017
No puedo estar más en desacuerdo con dicha opinión. Por ejemplo, cada día enviamos mensajes a través de Whatsapp, los cuales están “cifrados de extremo a extremo”, pura criptografía. Y la realidad es que existen multitud de actos cotidianos que utilizan implícitamente algoritmos y operaciones matemáticas.
Quizás por opiniones como las del tweet anterior, en los últimos años, numerosos docentes y divulgadores de matemáticas están (estamos) tratando de enseñar y comunicar las matemáticas de una manera más lúdica, como por ejemplo a través de sus aplicaciones en diversos aspectos de la vida cotidiana.
Existen multitud de actos cotidianos que utilizan implícitamente algoritmos y operaciones matemáticas
Este hecho me parece admirable a la par que curioso, pues a un docente de otra materia como pueda ser historia o lengua no se le exige, a priori, este esfuerzo por intentar hacer el temario “atractivo”. Parece que ahora no solo hay que educar, sino que también hay que entretener al alumnado.
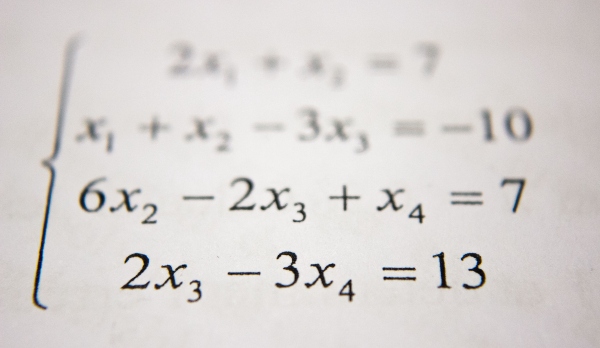
Un ejemplo de respuesta: el emprendimiento.
La realidad es que hay un abanico enorme de respuestas posibles a la pregunta del título “¿para qué sirven las matemáticas?”, pero nos centraremos en un ejemplo concreto dentro de la característica estrella de EDEM: el emprendimiento.
En 1996, los estudiantes de posgrado Larry Page y Sergey Brin de la Universidad de Stanford tenían una idea emprendedora, que era crear un motor de búsqueda de contenido en Internet. El objetivo era que el motor de búsqueda ofreciera una lista de páginas web de la World Wide Web relacionadas con la búsqueda realizada y ordenadas según su “grado de importancia”. Por tanto, Page y Brin tenían un problema a resolver: cómo clasificar las páginas web de acuerdo a su “grado de importancia”.

Tal y como se comenta en la Introducción del ebook Compendio de EDEM, “si podemos traducir un problema complejo a lenguaje matemático (ecuaciones), se podrá simplificar la realidad”.
Y precisamente esto fue lo que hicieron Page y Brin para convertir en realidad su idea emprendedora de desarrollar su motor de búsqueda: el conocido Google (se dice que pusieron este nombre por similitud a gúgol (googol en inglés), que es el nombre del número 10 elevado a 100, un número extremadamente grande).
⭐ Page y Brin son ingenieros. Si quieres conocer qué salidas laborales tiene una ingeniería no te puedes perder el post ¿Qué hace un ingeniero?
Modelización de un problema complejo: de las palabras a las ecuaciones.
Por tanto, la pregunta clave que se plantearon Page y Brin era la siguiente: ¿cómo medimos el grado de importancia de las páginas web?
Pues a través de dos sencillas ideas en las que todos estaremos de acuerdo: en primer lugar, una página web es importante si muchas otras páginas web envían enlaces a ella (i.e. cantidad de enlaces); o, en segundo lugar, si un reducido número de páginas web envían enlaces a ella, pero son páginas web “importantes” (i.e. calidad de los enlaces). Solo queda, por tanto, traducir este problema a lenguaje matemático y encontrar una solución.
Una estrategia que es muy útil en matemáticas es ponerse ejemplos sencillos y simplificados que ayuden a entender el problema en global, y si lo acompañamos con algún dibujo mucho mejor. Por ello, supongamos que tenemos que en la World Wide Web solamente existen 4 páginas relacionadas con cierta búsqueda que hemos realizado (las llamamos A, B, C y D) y cuyos enlaces están representados por la siguiente figura:
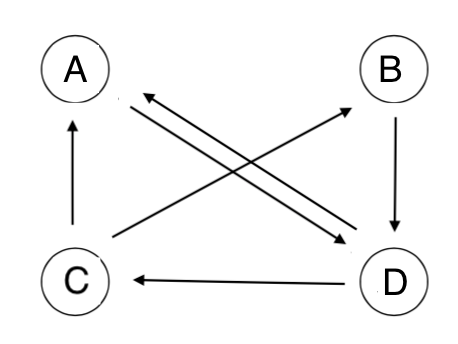
Esto quiere decir que la página A envía un enlace a la página D; B enlaza también a D; C enlaza tanto a A como a B y finalmente D enlaza a A y a C.
Primera idea transformada en una ecuación.
Como hemos comentado anteriormente, una página web es importante si recibe muchos enlaces de otras páginas (i.e. cantidad). Centrémonos por ejemplo en la página D, la cual recibe enlaces de las páginas A y B.
Por tanto, la importancia de D depende de las importancias que tengan las páginas A y B, y tiene sentido afirmar que la importancia de D aumentará conforme lo hagan las importancias de A y B. Deducimos así la ecuación I(D)=I(A)+I(B), donde I(X) es la importancia que tiene una página cualquiera X.
Ya tenemos una manera de medir la importancia de la página D. El objetivo ahora es obtener ecuaciones similares para I(A), I(B) e I(C).

Segunda idea transformada en una ecuación.
Por otro lado, la segunda idea trataba sobre la calidad de los enlaces. Supongamos ahora que la importancia de una página web se reparte por partes iguales entre las páginas a las que envía enlaces. Así, por ejemplo, si una página cualquiera X envía cuatro enlaces a cuatro páginas web distintas, entonces X entrega a cada una de ellas un cuarto de su importancia.
Traduzcamos esta idea ahora a lenguaje matemático. Podemos observar que la página B solo recibe enlace de la página C, luego la importancia I(B) solo depende de I(C). Pero, bajo la suposición del párrafo anterior, a la página B solo le llega la mitad de la importancia de la página C, pues C envía dos enlaces (a las páginas A y B, respectivamente). Así obtenemos que I(B)=I(C)/2. Análogamente, como C recibe enlace solo de la página D, la cual envía dos enlaces (a A y a C en este caso), deducimos que I(C)=I(D)/2.

La suposición que estamos realizando tiene sentido: por ejemplo, en el fútbol “tiene más mérito” marcar un gol si tiras solo una vez a portería que si tiras 1000 veces. Es decir, recibir un enlace de una página web que solo envía un enlace “tiene más mérito” (i.e. calidad) que recibirlo de una página que envía muchos enlaces.
Ambas ideas transformadas en una ecuación.
Con estos dos procedimientos a la vez (i.e. cantidad y calidad), podemos también sacar la última ecuación que nos falta, la relativa a la importancia de la página web A: I(A)=I(C)/2+I(D)/2, ya que A recibe enlaces de C y de D, las cuales a su vez envían dos enlaces y por tanto reparten por la mitad sus importancias.
El vídeo siguiente muestra de una manera muy visual la idea principal que hay detrás de este modelo:
La resolución del problema.
Ya tenemos por tanto “lo que nos gusta”, un sistema de cuatro ecuaciones lineales con cuatro incógnitas (las importancias de A, B, C y D).
No vamos a entrar en detalles de cómo resolverlo, pero tal y como explicamos en clase, podemos comprobar que se trata de un sistema compatible con infinitas soluciones y podemos expresar todas estas infinitas soluciones como múltiplos del siguiente vector de probabilidad (i.e. cuyas entradas suman 1):
(I(A), I(B), I(C), I(D)) = (0.3, 0.1, 0.2, 0.4).
Es decir, si multiplicamos estos números por 2, por 10 o por 1000, siempre existirá la misma proporción entre ellos y siempre serán soluciones de las ecuaciones que hemos obtenido anteriormente. Por tanto, la página web más importante y que primero mostraría Google sería la D, seguido de la A, luego la C y finalmente la B.
Esta es solamente la idea principal y simplificada del algoritmo inicial que usaron Page y Brin, el cual es conocido como PageRank y actualmente está patentado. ¿Para qué sirven las matemáticas? Pues por ejemplo para crear este algoritmo que ha revolucionado Internet y ha ayudado a miles de millones de personas. Por supuesto, este proceso ha ido sufriendo diferentes mejoras y modificaciones hasta la actualidad.
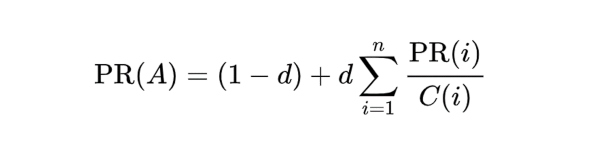
Por comentar alguna de ellas, evidentemente no siempre navegamos por la web a través de enlaces de unas páginas a otras, sino que a veces tecleamos directamente en el navegador alguna dirección concreta. Pero esta idea también se puede modelar matemáticamente a través de probabilidades. Y realmente lo más increíble de Google es que es capaz de realizar miles de operaciones de este tipo con cientos de millones de páginas web de la World Wide Web, ¡en milésimas de segundos! Impresionante.
Tal y como vemos en las clases de Álgebra del Grado en Ingeniería y Gestión Empresarial de EDEM, este ejemplo es muy interesante pues nos permite engranar diferentes conceptos matemáticos que estudiamos en dicha asignatura, como los valores y vectores propios, las matrices estocásticas, los vectores de probabilidad, las cadenas de Markov, etc., nociones que además poseen una gran cantidad de aplicaciones en otros campos.
El caso del algoritmo de Google es un ejemplo para explicar diferentes conceptos matemáticos
Y efectivamente, como estarás pensando, este es uno de los trucos con los que intento mantener “entretenido” al alumnado.
¿Para qué sirven las matemáticas? La eterna respuesta y la moraleja.
Larry Page y Sergey Brin se formaron en Ciencias de la Computación en la Universidad de Stanford, donde en particular estudiaron los diversos conceptos que acabamos de mencionar.
Page y Brin podrían haber escrito un tweet similar al comentado al inicio de este post, como pudiera ser “otro día más sin resolver un sistema de ecuaciones lineales”, y hubiesen conseguido seguramente levantar algunas risas entre su círculo social. Pero fueron más allá y aplicaron estos conceptos para hacer realidad su idea de negocio.

Así pues, podríamos decir que gracias a que un día sí que supieron utilizar dichos conceptos, hoy en día son dos de las personas más ricas del mundo. Son un ejemplo claro de para qué sirven las matemáticas.
Larry Page y Sergey Brin demostraron nítidamente para qué sirven las matemáticas al desarrollar un motor de búsqueda que ha facilitado el acceso a la información en Internet
Además, esta última afirmación me hace recordar una “eterna” paradoja que conocí a través del profesor de EDEM Felipe Sánchez: ¿cuál es la retribución que han logrado Page y Brin por unas determinadas horas de trabajo? ¿Es justo? ¿O es porque hicieron algo que ayuda a millones de personas todos los días? Juzguen ustedes mismos.











