En los últimos años, las matemáticas están siendo aplicadas en gran cantidad de sectores laborales y ello hace que su relevancia esté creciendo exponencialmente.
En España, las matemáticas son directamente responsables de más de un millón de empleos (un 6% del total) y las actividades con intensidad matemática generan un 10% del PIB, según un informe de la consultora AFI en 2019.
Dentro de las matemáticas, las ecuaciones diferenciales son una gran herramienta por sus innumerables aplicaciones en otras disciplinas.
¿Qué es una ecuación diferencial?
En términos generales, una ecuación diferencial es una ecuación que involucra a las derivadas de una función con la propia función y/o las variables de las que depende. En sus aplicaciones, las funciones generalmente representan cantidades y las derivadas son las tasas de variación de estas cantidades.
¿Por qué son útiles las ecuaciones diferenciales?
Estas relaciones entre cantidades y sus tasas de cambio son frecuentes en áreas como la Física, la Biología, la Ingeniería o la Economía. Existe una gran cantidad de fenómenos reales complejos que pueden ser formulados en términos de ecuaciones diferenciales, lo cual permite predecir sus comportamientos futuros, entre otras cosas.
⭐ Si quieres conocer qué salidas laborales tiene una ingeniería no te puedes perder el post ¿Qué hace un ingeniero?
Por tanto, las ecuaciones diferenciales permitieron a estas ciencias pasar de ser empíricas a ser descriptivas y predictivas.
Algunos usos de las ecuaciones diferenciales en la vida real
Uno de los ejemplos más recientes lo encontramos el pasado año, cuando se intentó predecir mediante el uso de ecuaciones diferenciales cuándo se doblegaría la curva de infectados durante la pandemia provocada por la COVID-19.
En el e-book Compendio de EDEM, podemos encontrar un excelente artículo introductorio a estos modelos matemáticos aplicados a la epidemiología y su adaptación al marketing viral y a la predicción del éxito de las campañas publicitarias.
Las ecuaciones diferenciales también pueden describir cómo cambian las poblaciones, cómo se transfiere el calor, cómo se desintegra el material radiactivo, etc. Como curiosidad, también sirvieron para determinar la causa del derrumbe del puente colgante de Tacoma Narrows (de casi un kilómetro de largo) en Washington en 1940.

En definitiva, las ecuaciones diferenciales son una forma muy natural de describir muchas cosas en el universo. Como dijo el matemático Alan M. Turing:
“Science is a Differential Equation”
Queda de manifiesto, por tanto, que las ecuaciones diferenciales (y las matemáticas en general) deben ser una pieza fundamental en la formación de un/a universitario/a STEM (Science, Technology, Engineering and Mathematics).
Ejemplo en términos matemáticos
Veamos un caso en términos matemáticos.

Las ecuaciones diferenciales pueden tener más de una solución. Por ejemplo:
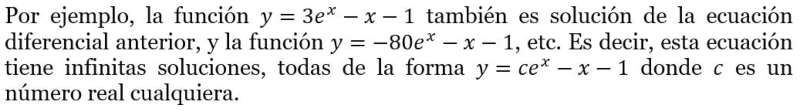

Ejemplo en redes sociales
Veamos un gracioso y sencillo ejemplo de aplicación de las ecuaciones diferenciales en el sector de las redes sociales.
Supongamos que el número de seguidores de una cuenta en Instagram crece de manera proporcional al número de seguidores que posee.

En otras palabras, tenemos la ecuación diferencial

Es decir, habríamos duplicado ampliamente el número de seguidores.
Primero clasificar, después (intentar) resolver
Con el paso del tiempo, célebres científic@s obtuvieron métodos específicos para resolver algunos tipos de ecuaciones diferenciales. Por ejemplo, la ecuación diferencial asociada al ejemplo anterior se puede resolver utilizando el conocido método de separación de variables, ya que se puede reescribir de la forma
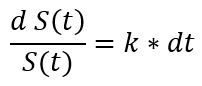
donde cada variable (es decir, la dependiente S(t) y la independiente t) aparece en un lado de la ecuación.
Otros tipos de ecuaciones diferenciales son las exactas, las lineales (como la del ejemplo en términos matemáticos visto al inicio), las homogéneas, las de tipo Bernoulli, etc. Por tanto, es fundamental identificar primero el tipo de ecuación diferencial que tenemos antes de intentar resolverla.
Es como cuando uno viaja: diferentes medios de transporte pueden ayudarte a llegar a ciertos destinos. Por ejemplo:
- ¿Está cerca y podemos ir andando?
- ¿Hay una carretera y podemos ir en coche?
- ¿Está en otra galaxia y aún no podemos llegar allí?
¡No siempre es fácil resolver las ecuaciones diferenciales!
Las ecuaciones diferenciales son una gran herramienta matemática para describir situaciones o fenómenos reales, pero para que sean realmente útiles necesitamos saber resolverlas y no todas tienen solución.
“Para que las ecuaciones diferenciales sean útiles necesitamos saber resolverlas”
Además, incluso en el caso de que exista solución, puede que esta no tenga una forma cerrada, i.e. que se pueda obtener por medio de operaciones algebraicas básicas. En tal caso, lo que se suele hacer es buscar computacionalmente aproximaciones de la función-solución mediante métodos numéricos.
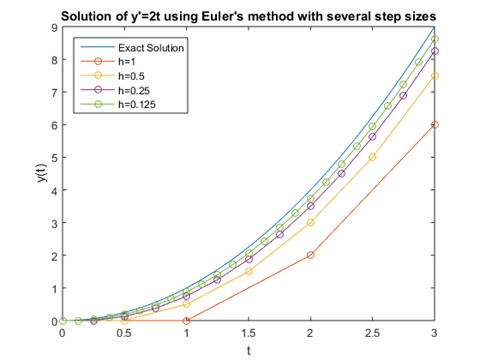
En otras ocasiones, el objetivo no es obtener la función en sí, sino que simplemente interesa saber propiedades cualitativas de la función. De hecho, este es un amplio campo de investigación en Matemáticas con una profusa participación de investigadores de todo el mundo.
Y todo esto solamente es un pequeño resumen de lo que vemos en la asignatura Ecuaciones Diferenciales del Grado en Ingeniería y Gestión Empresarial de EDEM.











