Una de las preguntas que más inquieta a un profesor de matemáticas es la de encontrar aplicaciones prácticas a los resultados que se desarrollan en las clases magistrales. Así sucede con el cálculo diferencial.
Si bien los asistentes a la lección pueden desconocer las aplicaciones que tienen en ciencia y tecnología, y que su comprensión es fundamental para el adecuado aprendizaje futuro y formación del alumno, los mismos asistentes pueden encontrarse que la tabla de derivadas no es de vital importancia a la hora de ir a hacer tareas rutinarias, tales como la compra semanal en un supermercado.
No obstante, mencionando el cálculo de las derivadas, existe una importante cantidad de ejemplos cuyos fundamentos descansan sobre una sólida base matemática, y que hasta la fecha no hemos reparado en ellos.
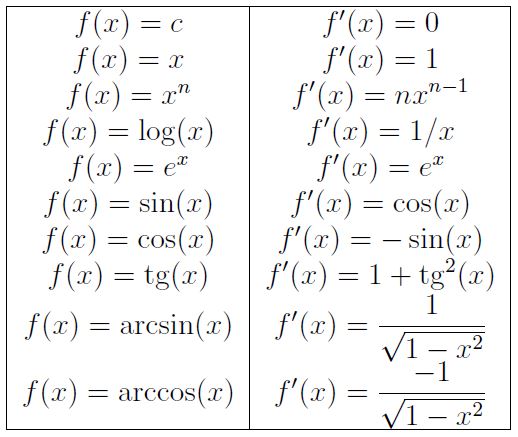
Veamos tres usos del cálculo diferencial en la vida cotidiana.
1. Cálculo diferencial en las relaciones personales
Debe haber una cantidad muy pequeña de ejercicios más cotidianos y rutinarios que la convivencia con una persona: familiares, un desconocido, tu mejor amigo o tu pareja. De hecho en ocasiones, notamos como nuestro comportamiento puede cambiar, incluso periódicamente: es posible que tengamos un par de meses de una relación estupenda, que los dos posteriores la convivencia se vea dificultada y así sucesivamente.

Modelicemos la cuestión matemáticamente: para ello, necesitamos el uso de funciones. Consideremos t como el tiempo que transcurre, y llamemos a f(t) y g(t) las funciones que miden nuestra amabilidad, interés, etc. hacia la otra persona, y la amabilidad, interés, etc. de la otra persona hacia nosotros, respectivamente, dependiendo del tiempo t. Parece razonable pensar que si nuestro compañero se siente apreciado, su interés aumentará hacia nosotros; y, por contra, si no se siente valorado, su estima decrecerá.
Con ello, la variación de su estima coincide con lo que aportamos. Las derivadas, al ser la variación de la función respecto a una variable, aparecen en la expresión acabada de mencionar. Matemáticamente, esto se escribiría como:
g'(t) = f(t).
Pongamos por contraposición que somos desconfiados por naturaleza: de esta manera, si la otra persona tiene demasiada estima hacia nosotros, caemos en la tentación de sospechar que está ocultando alguna cosa, y que consecuentemente nuestro aprecio hacia la otra persona decrece. Además, si resultamos ser aquellos a los que una persona fría nos cae bien, nuestro interés hacia él aumentará con dicho comportamiento. Con ello, tendríamos que:
f'(t) = -g(t).
Notemos, con la tabla de derivadas, que las funciones trigonométricas
f(t) = cos(t), g(t) = sin(t)
cumplen el sistema de ecuaciones y resolverían el problema modelizado, utilizando conceptos básicos de cálculo diferencial.
2. Cálculo diferencial en la enseñanza
Otra de las tareas rutinarias es asistir a los centros educativos, donde los alumnos obtienen conocimientos acerca de varios temas. Este debe ser el objetivo primordial que persigue un profesor.
Pensemos que el profesor trata de enseñar de una manera lineal. En este caso, la velocidad de aprendizaje será constante. La tabla de derivadas nos dice que la función x modeliza la adquisición de conocimientos mediante este mecanismo.

Pero, más allá de mostrar el material creado por el profesor, se puede motivar al alumno a que profundice su interés. Así que podríamos decir que con una mayor motivación en la asignatura, ellos podrán aprender a un ritmo mayor. Este nuevo método metodológico seguiría el modelo de la función x2.
Un paso más allá sería el de, no solo motivar en una asignatura al alumno, sino que aprendiese a automotivarse: que adquiera a nutrir sus propios intereses en algún aspecto concreto. Esta manera de aprendizaje podría ser similar al de la función x3.
La mejor manera para enseñar es dando conocimiento básico sobre los conceptos, que luego adquieran motivación por el concepto, para que en una tercera fase sean capaces de automotivarse.
¿Por qué?
Si observamos, en fases muy iniciales del aprendizaje, la función que tiene un mayor crecimiento es la función x, que luego, a un cierto punto, es sorpassada por x2 , y por x3 .

3. Cálculo diferencial en la empresa
Para los empresarios, el dirigir una empresa se trata de la cuestión más importante y que ocupa sus mentes durante todas las horas de un día. En particular, el buscar que la empresa sea solvente es la primera cuestión. Pero yendo más allá, lo que cualquiera debe proponerse es lograr optimizar sus beneficios, mediante sus proyectos.
Obtener un óptimo se basa en la búsqueda de un mínimo o de un máximo para algún valor que tenga sentido en el problema dado. Para ello, existe una gran variedad de herramientas (matemáticas) que sirven de gran ayuda para ello.
“Las derivadas de las funciones son una de las herramientas más usadas y más potentes”
Efectivamente, la manera de conseguir optimizar el beneficio de cualquier empresa sigue las líneas del ejemplo de la enseñanza. De acuerdo con el anterior estudio, haciendo la casuística análoga, la mejor manera de proceder debería ser, una vez se empieza a dirigir el negocio, a no perseguir el máximo beneficio: este, si se ha procedido con esfuerzo y de una manera correcta y adecuada, llegará en fases más avanzadas del proyecto.
Conclusión
La conclusión que podemos extraer es que no existe el conocimiento inocuo: cada uno de los resultados adquiridos forman parte del aprendizaje, y que todos ellos pueden ser aplicados en un rango muy amplio de situaciones.
“No existen los conocimientos inocuos, todos ellos pueden ser aplicados”
Las derivadas nos han permitido realizar, entre otras cosas, modelizaciones de problemas en los que se involucre un cambio con el objetivo de hacer predicciones, en busca del óptimo.
Si estas complejas herramientas han sido capaces de explicar ejemplos prácticos rutinarios, ¿de qué no serán capaces?












